Physics Lournal
Powered by 🌱Roam GardenThe Nature of Classical Physics
Classical Mechanics focuses on physical systems that are deterministic, and reversible.
By deterministic, what we mean is that there are a set of logical rules that allow you to derive the state of the future, given its current state.
By reversible, we mean that given the state of the system at some point in the future we should be able to derive the state of the system at some point in the past.
By system, we mean a collection of objects.
A system can be considered closed, if it is isolated from the effects of agents and events external to the system. Any system that is not closed, is open.
Realistically speaking, there is no such thing as a truly closed system, only approximations.
Most systems possess chaos, or can be considered chaotic, because slight changes in initial conditions, drastically alter the evolution of the system. The property of chaos puts a limit on how far into the future we can reliably predict the evolution, or state of a system.
The Three Body Problem is a great example of this: if we increment the number of components in a gravitational, orbital system by one (1), we suddenly can't predict the evolution of any of the components of the system, meaning we can't predict the evolution of the system.
We talk about the evolution of systems, in terms of states: the set of all possible states a system can be in is called the state-space.
We also assume that the evolution of a system will take place in a smooth manner, without sudden jumps or interruptions, often summed up in the term continuous.
We can treat time as discrete, usually represented by , where the value of is indexed to the integers.
When a world has a discrete evolution, or time interval, we can call it stroboscopic.
When we deal with time, and how a system changes with respect to it, we are dealing with a Dynamical System.
A Simple System:
A coin is a very simple system, with two possible states: .
The first and most simple dynamical law simply states that if nothing happens, the state of the system remains the same, or as Albert Einstein said:
Going beyond this, we can say, in terms of a coin, the next state is the opposite of the current state:
These dynamical laws can be written in equation form, and additionally, each variable describing a system is a degree of freedom.
In the case of the coin, there's a single degree of freedom, which can be represented by sigma (), which has two values, 1, or -1, respectively.
If we are considering the evolution of the system over time, we introduce a new variable to represent its value at some time- if time is continuous, if it discrete.
Because we can predict the state of the system at any point in the future, with the state of the system being determined by the initial conditions, these laws are deterministic.
We can increase the complexity by considering a six sided die, which greatly increases the number of possible dynamical laws and associated equations.
For instance, we can cycle through each side of the die, which is 6 different states, however once we get to the 6th state, we have to go back to one, a process referred to as a cycle.
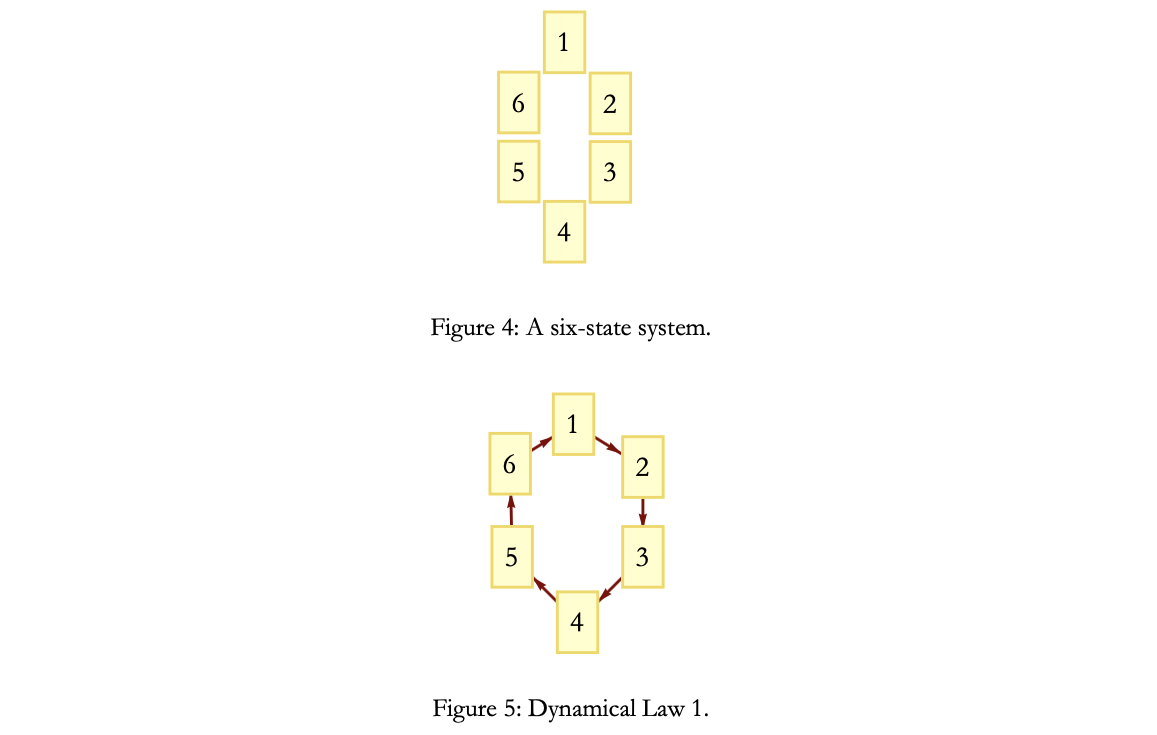 Cycling through the states of a six sided die system.
Cycling through the states of a six sided die system.
It's important to note that the direction of the cycling does not not necessarily indicate a different physical system. The states of the system and degrees of freedom haven't changed even though the ordering of the cycling through states have.

However, it is equally important that even though the states of the system may not change, the way they are cycled through can represent a different system, one that is not logically equivalent.
 This system has the same states, but two cycles, and you can't reach every state of the system, from any other state.
This system has the same states, but two cycles, and you can't reach every state of the system, from any other state.
Rules That Aren't Allowed
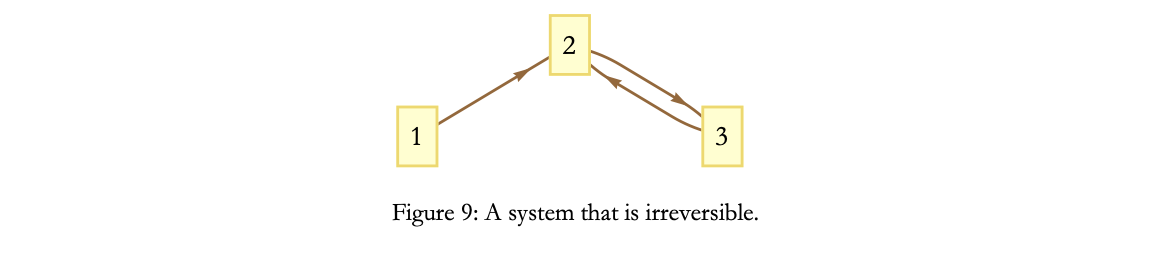
Classical Physics does not just require the dynamical laws of physical systems be deterministic, it also requires them to be reversible.
Consider this six sided die system: