In Mathematics, topology is concerned with the properties of geometric objects under continuous deformations.

A topological space, is a set theoretic structure, that allows for continuous deformation of subspaces (subsets of the superspace!).

The aspect of a surfaces nature, which is unaffected by deformation, is called the topology of the surface.

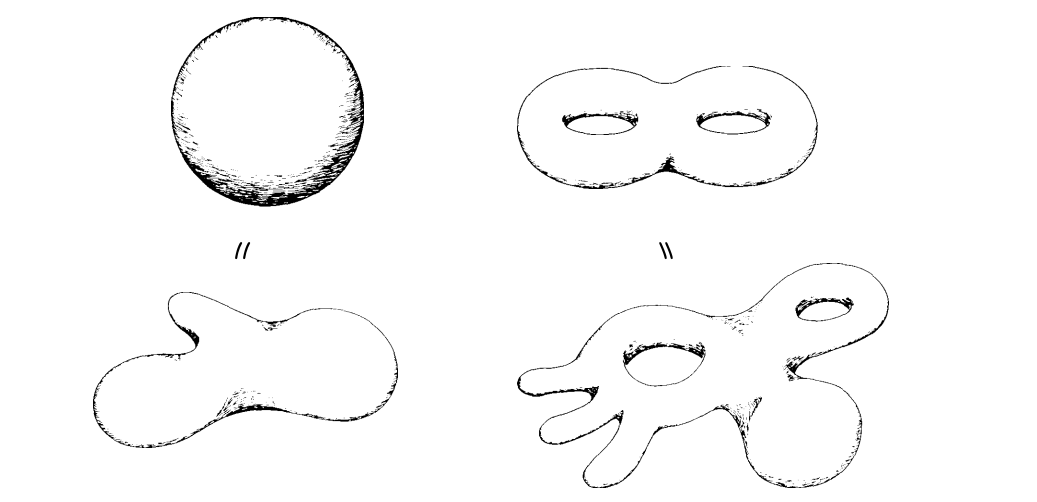
The two surfaces on the left, have the same topology, as do the two on the right, however, the sphere and two holed doughnut have different topologies: one can never be deformed into the other (without topological tearing, or gluing).

The aspects of a surface that do change under deformation are the surface's geometry.

Curvature is the most important geometric property.

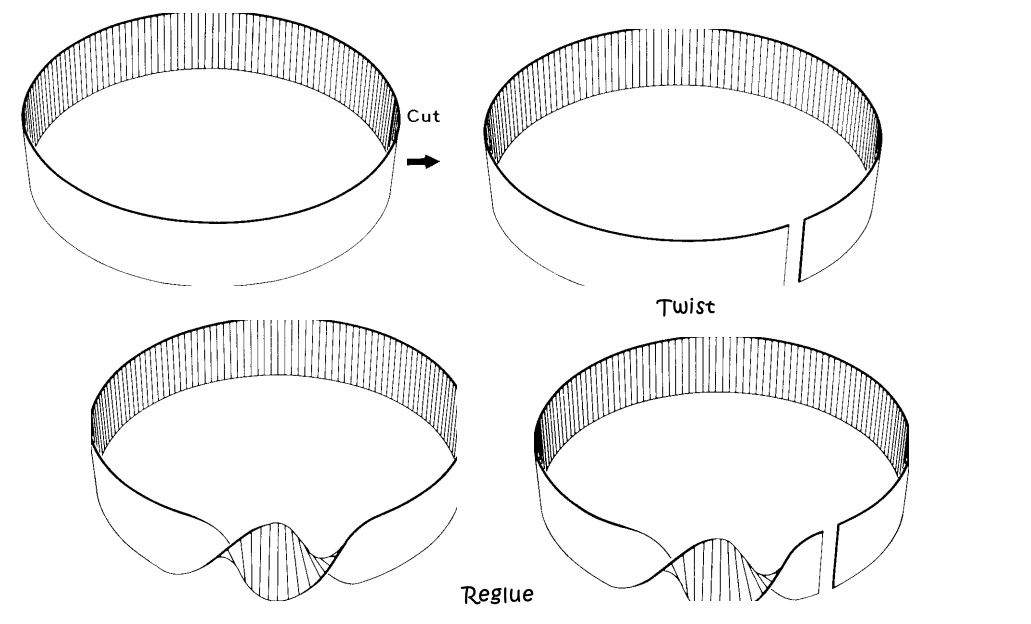
The figure below shows how to twist a rubber band- to us, it is topologically different, but it would seem no different to a two dimensional creature.

This is because the intrinsic topology of the band has not changed, but it's extrinsic (the way it's embedded in 3D space) topology has changed.

Two surfaces have the same intrinsic topology if Flatlanders cannot tell the difference between an original and deformed surface.

Two surfaces have the same extrinsic topology if one can be deformed within 3D space to look like the other.