Physics Lournal
Powered by 🌱Roam Garden1.2 Spins and Qubits
The concept of Spin, is one of a fundamental property of fundamental particles. A heuristic for visualizing this is an arrow pointing in the direction of the spin, but there is no real classical analogue.
Spin is a quantum system in its own right, and is an example of the systems referred to as qubits.
1.3 An Experiment
In TM:CM, there was an example of a coin as a two state system, with a state space of or .
Formally, we take a degree of freedom, , and we can speak about the system in terms of this degree of freedom:
In the classical context, this is all thats needed to talk about the state space of the system.
There's also an evolutionary law describing the changes between states: , if nothing happens, and if things do change.
That being said, this example contains a hidden assumption, because there's more involved than the system we're measuring the state of.
There was a hidden apparatus, , that measures the system *for us*, and stores the results of that measurement.
Apparatus can be envisioned as below, interacting with the spin, our qubit, and records the value of . is labeled according to how it should be oriented in space, as well as having a screen to read out the measurement. Initially, we begin with the apparatus aligned with the z-axis.
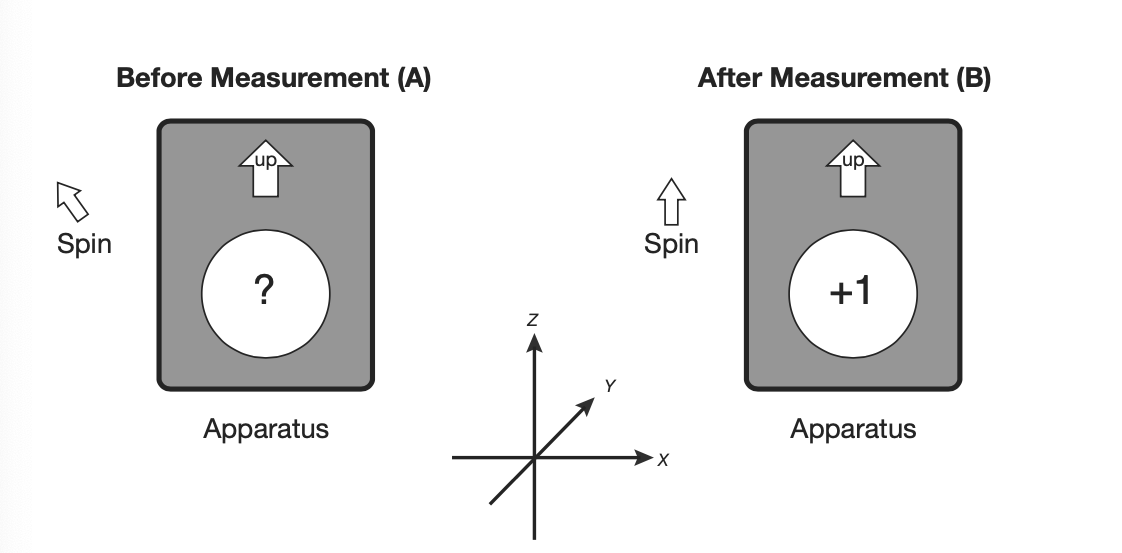
Initially, we have no knowledge of the value.
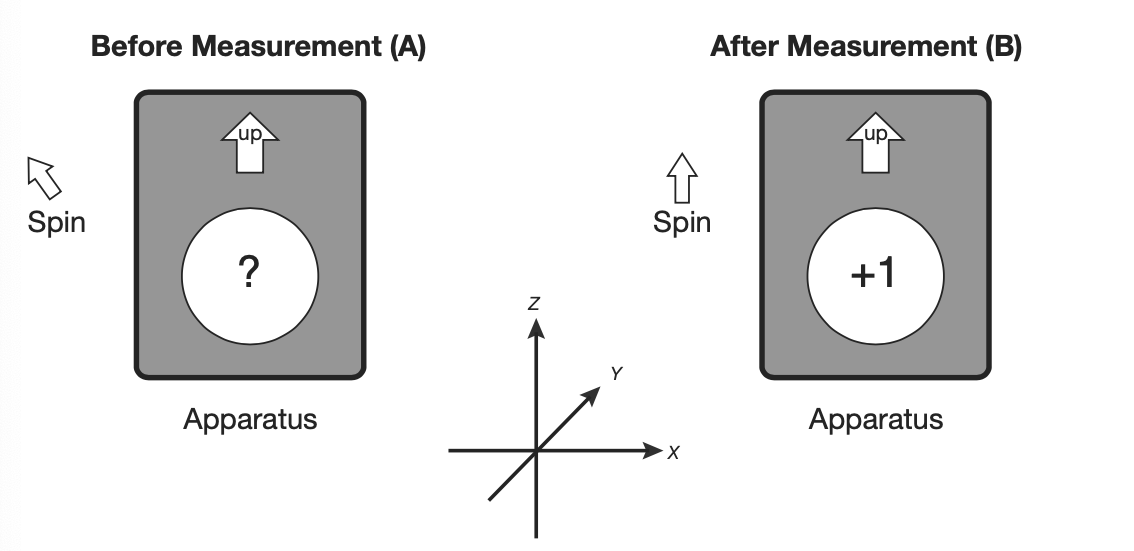
After the measurement, we see that the state of the system is , or put another way, the state of our spin qubit is up.
Were we to take this apparatus and retake our measurement, we would get the same result, provided no serious disturbances occur.
From this we can observe that the first interaction of , with the system, places the system in one of the two states, and following measurements of the system confirm the state.
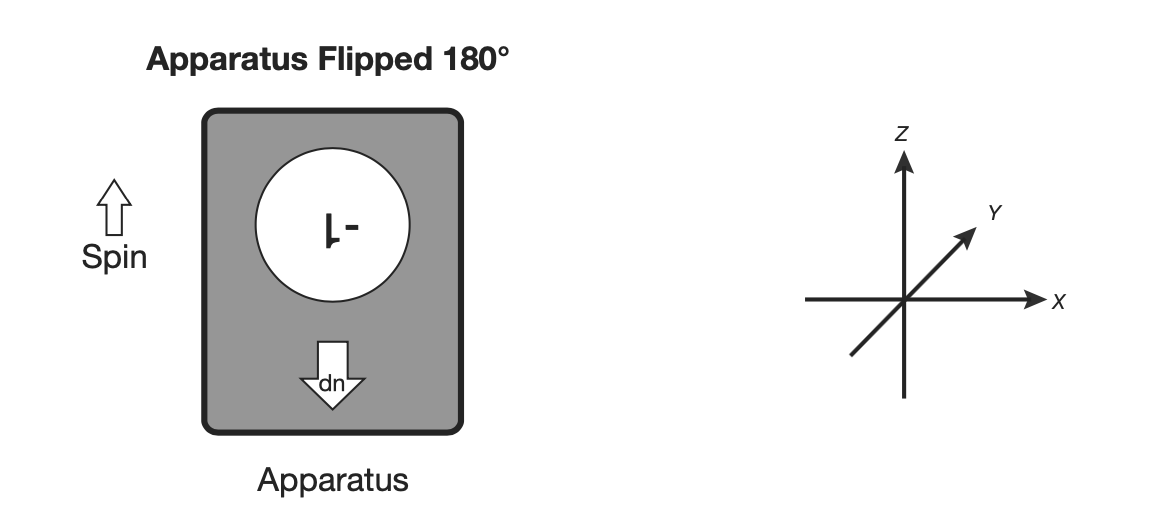
If we flip the apparatus, without disturbing the state of the qubit, it will measure .
From this, we can conclude that our degree of freedom, sigma (), is associated with spatial orientation. If sigma represented a vector, this would be the natural expected result. We can conclude that perhaps the apparatus measures the component of the vector that exists along the z-axis.
If we assume that the spin exists as a vector, we would describe it according to it's components: .
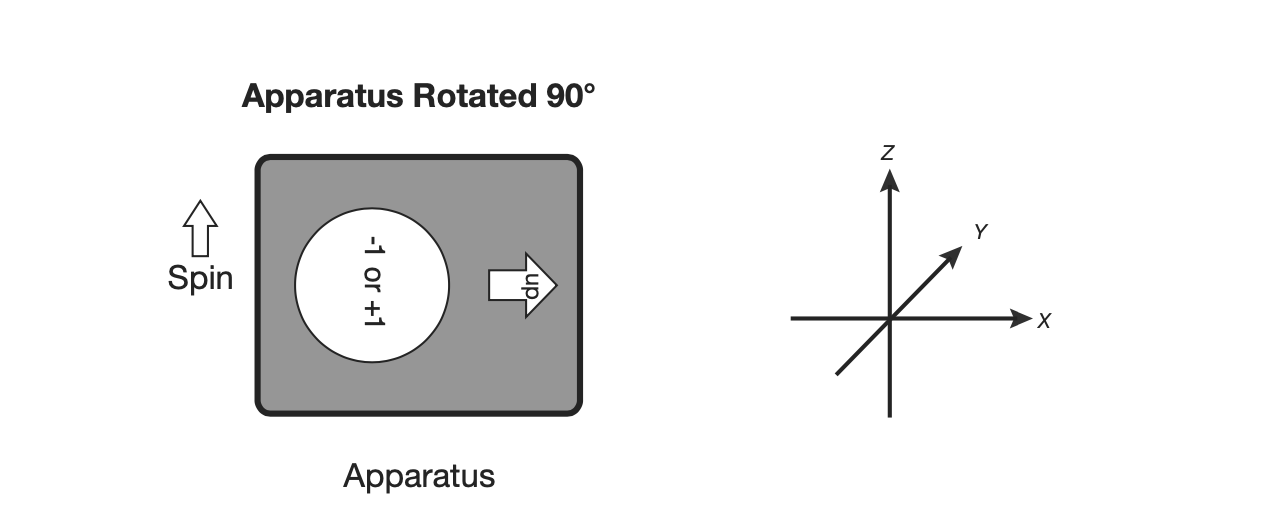
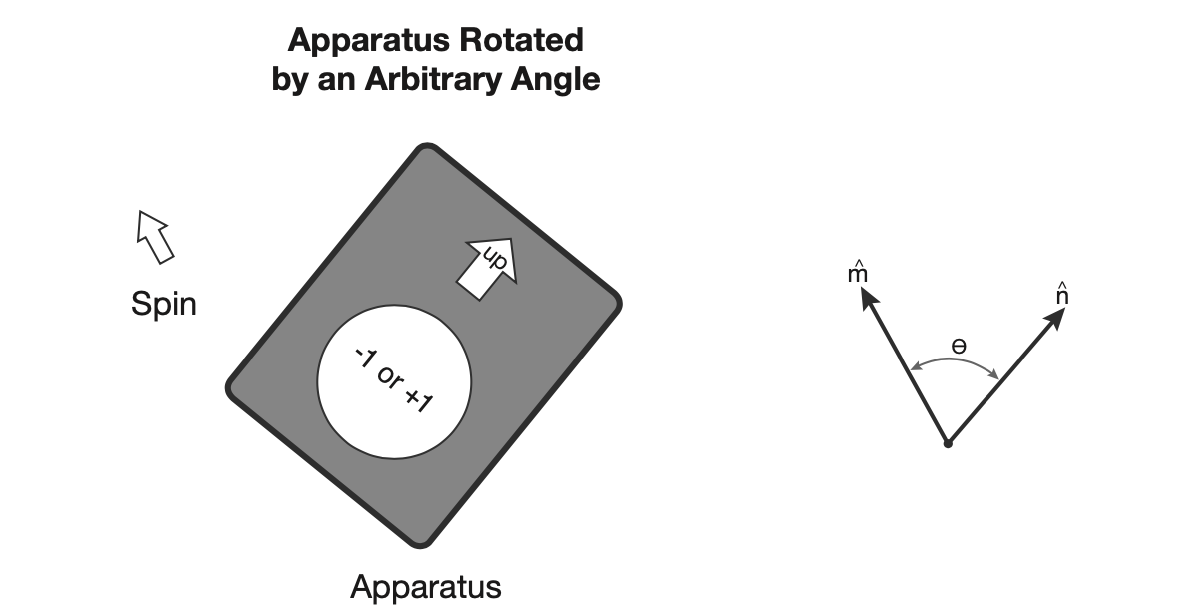
Rotating the apparatus by , and measurement results in with a probability.
So far, these measurements line up with classical expectations, however, the inconsistency will reveal itself if we rotate the apparatus by an arbitrary number of degrees, such as , and take a measure of the component of the vector that lies along the x-axis.
What we would expect, is that we would get zero, if represents a degree of freedom along the z-axis, because we confirmed that it lies along that axis in prior experiments.
However, what occurs, is that , which would be a very peculiar vector.
If we repeat this procedure, preparing along the z-axis, and measuring then we notice something: we get a series of relatively random measurements, of +1 or -1, but over time, it will converge along the statistical expectations, with the measurements being split 50/50 between +1 or -1, however this is not a replacement for classical results: instead of measuring 0, we find that the average of repeated measurements is 0.
From here, we go back to squre one, and rotate along the unit vector . Classically, if was a vector, the apparatus should measure the component of it that lies along the axis. If this vector lies at some angle , with respect to the z-axis, the measurement would be .