Physics Lournal
Powered by 🌱Roam GardenLecture 1 - Systems and Experiments
1.1. Quantum Mechanics Is Different.
Part of the difficulty of quantum mechanics, lies in the advancement of the involved mathematics, but the real complication is that the concepts therein apply to objects that exist at scales we can't perceive.
It is non-intuitive in terms of our *sensory perception*.
You're a slave to your own neural architecture.
While Classical Mechanics does contain phenomena of the same nature, there are two key ways that QM diverges:
1. QM relies on unique abstractions, and different mathematical structures, with different logical configurations.
2. States and measurements behave differently: Classically, there's a straightforward relation between the states of a system, and measurement of that system. The labels that define states, *are the same as the labels of measurement*.
1.2 Spins and Qubits
The concept of Spin, is one of a fundamental property of fundamental particles. A heuristic for visualizing this is an arrow pointing in the direction of the spin, but there is no real classical analogue.
Spin is a quantum system in its own right, and is an example of the systems referred to as qubits.
1.3 An Experiment
In TM:CM, there was an example of a coin as a two state system, with a state space of or .
Formally, we take a degree of freedom, , and we can speak about the system in terms of this degree of freedom:
In the classical context, this is all thats needed to talk about the state space of the system.
There's also an evolutionary law describing the changes between states: , if nothing happens, and if things do change.
That being said, this example contains a hidden assumption, because there's more involved than the system we're measuring the state of.
There was a hidden apparatus, , that measures the system *for us*, and stores the results of that measurement.
Apparatus can be envisioned as below, interacting with the spin, our qubit, and records the value of . is labeled according to how it should be oriented in space, as well as having a screen to read out the measurement. Initially, we begin with the apparatus aligned with the z-axis.
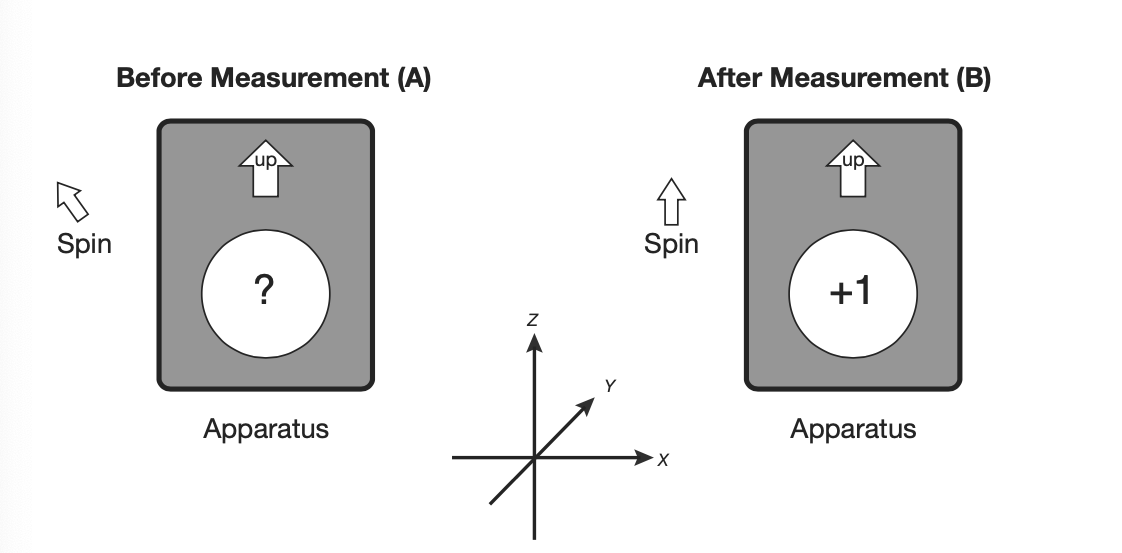
Initially, we have no knowledge of the value.
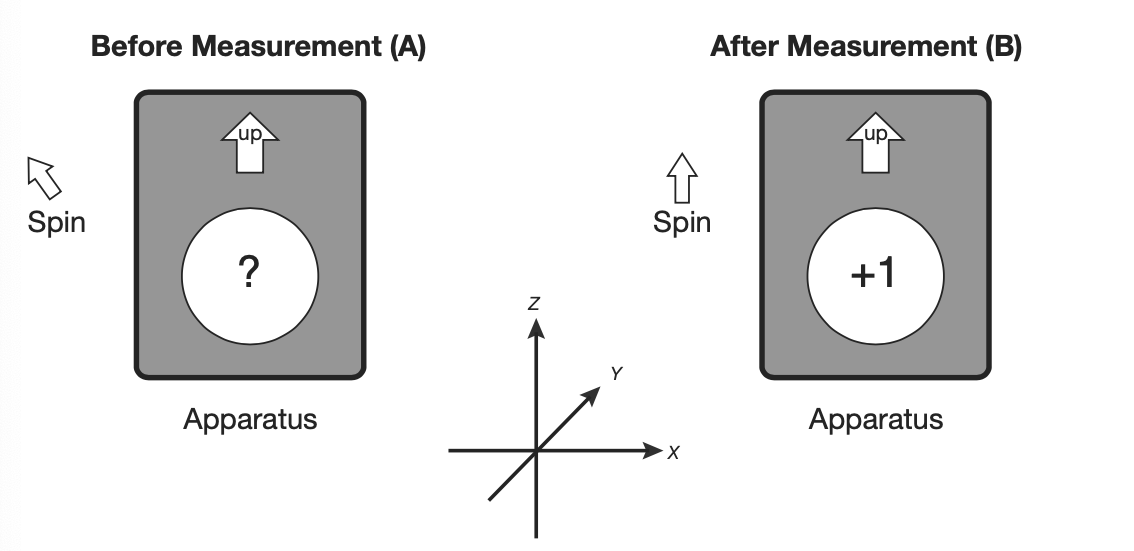
After the measurement, we see that the state of the system is , or put another way, the state of our spin qubit is up.
Were we to take this apparatus and retake our measurement, we would get the same result, provided no serious disturbances occur.
From this we can observe that the first interaction of , with the system, places the system in one of the two states, and following measurements of the system confirm the state.
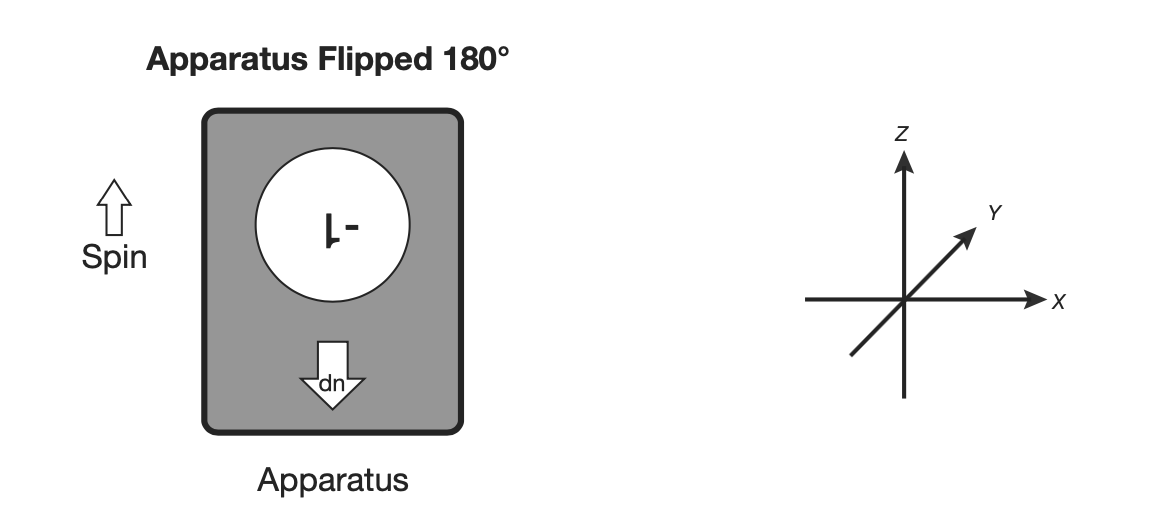
If we flip the apparatus, without disturbing the state of the qubit, it will measure .
From this, we can conclude that our degree of freedom, sigma (), is associated with spatial orientation. If sigma represented a vector, this would be the natural expected result. We can conclude that perhaps the apparatus measures the component of the vector that exists along the z-axis.
If we assume that the spin exists as a vector, we would describe it according to it's components: .
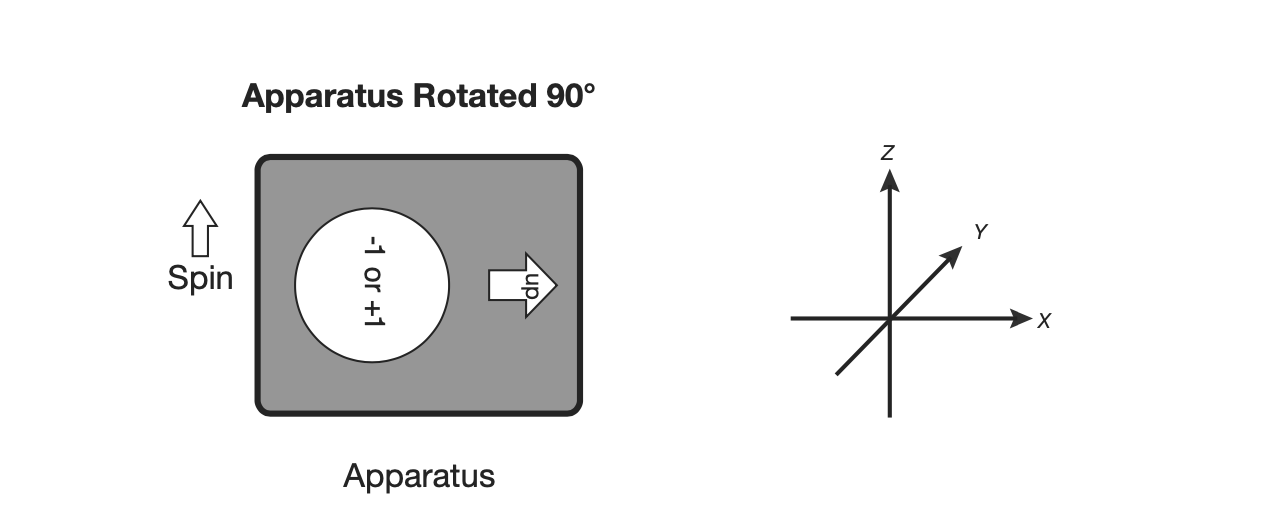
Rotating the apparatus by , and measurement results in with a probability.
So far, these measurements line up with classical expectations, however, the inconsistency will reveal itself if we rotate the apparatus by an arbitrary number of degrees, such as , and take a measure of the component of the vector that lies along the x-axis.
What we would expect, is that we would get zero, if represents a degree of freedom along the z-axis, because we confirmed that it lies along that axis in prior experiments.
However, what occurs, is that , which would be a very peculiar vector.
If we repeat this procedure, preparing along the z-axis, and measuring then we notice something: we get a series of relatively random measurements, of +1 or -1, but over time, it will converge along the statistical expectations, with the measurements being split 50/50 between +1 or -1, however this is not a replacement for classical results: instead of measuring 0, we find that the average of repeated measurements is 0.
From here, we go back to squre one, and rotate along the unit vector . Classically, if was a vector, the apparatus should measure the component of it that lies along the axis. If this vector lies at some angle , with respect to the z-axis, the measurement would be .
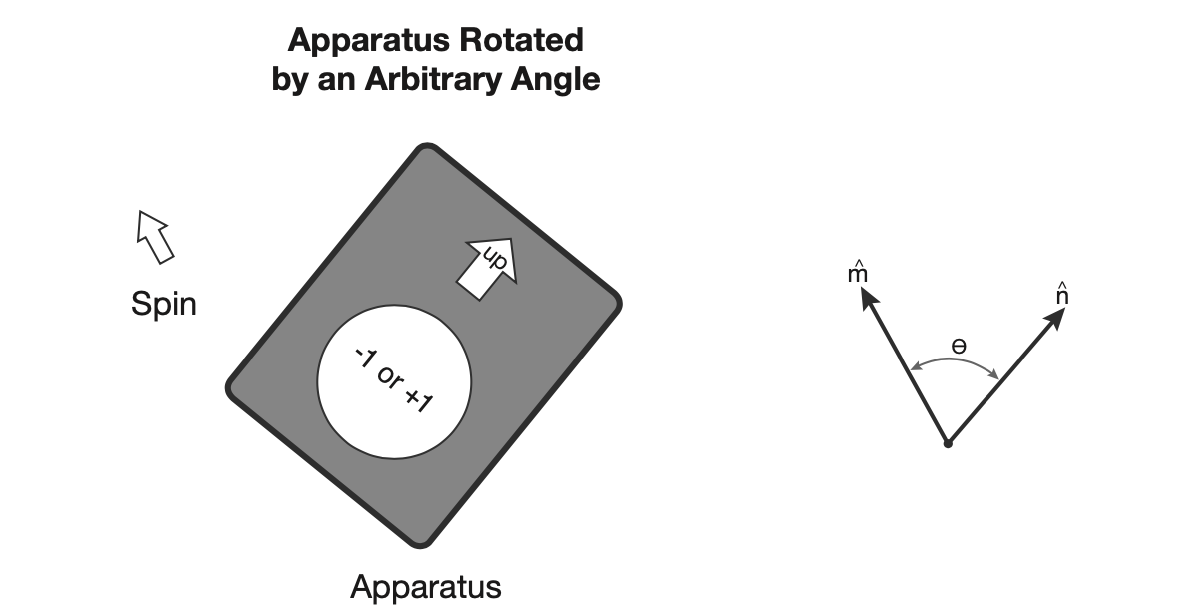
We use , as the "hat" indicates that we're dealing with a unit vector, or a vector of length one.
However, the result again, is random, with , but the average of these measurements do statistically converge on .
This situation can be generalized: Pick any unit vector , and prepare a spin of +1, and rotate the apparatus to lie along , and measure the vector, and you will get a random series of results but with an average equal to the cosine of the angle between and .
The mathematical notation for the statistical average of some quantity is Dirac's bra-ket notation ().
This allows us to summarize the results of the experiments as follows: if we begin with along some axis and prepare a spin of , then orient along , and take measurement, the statistical value is .
Effectively, quantum systems behave non-deterministically, with statistically random results, but repetition of experiments, provides results that match classical physics, up to a point.
1.4 Experiments Are Never Gentle
All experiments require interaction wth some outside system, meaning every experiment is, to some degree, invasive. Classicaly, measuring apparatuses have negligible effects on the systems they measure, and thus can be considereds "arbitrarily gentle".
In QM, the situation is fundamentally different, in that any interaction with a system that is strong enough to measure an aspect of it, is necessarily strong enough to destroy some other aspect of the system.
You can not remove information from a quantum system for free.
Considering apparatus , between measuring along the z-axis, we rotate the apparatus , and then rotate it back to lie along the z-axis: after this, our measurement will not confirm the previous measurements along this axis, and will again begin returning random values or .
There is no way to take intermediate measurements, without altering the results of the final measurement. It is as if measuring the component of this vector along some axis, destroys the information about another component of the vector.
Testing Quantum Propositions
Assuming an agent was preparing the apparatus with a spin of .
This makes the proposition (+1 or -1), true, and we needn't go further- however if we did measure the spin along , we would get our typical random, yet statistically classical results, that wouldn't change the truth value of our proposition.
: the z component of the spin is +1 or the x component of the spin is +1.
From here though, we can imagine reversing the proposition, to , and then measuring , knowing that is +1.
In the event that , the statement in our reversed proposition is true, and in the fashion of logical or statements, we don't check $A$.
However, if we find that , the vector is now along the -x axis, and the proposition that works in all cases in one direction, is unworkable in the other direction: a sort of commutativity has been lost as a result of our measurement.
Given than , representing X, can be -1, we end up in a situation where there's a 25% chance, that upon measurement, this proposition will be false.
This means that not only are the laws of quantum physics different, but the very logic of it is as well.
We run into a similar problem, with , where upon measuring one statement, regarding the spin of some qubit vector along the prepared axis, we get only random answers regarding the alternative statement.
, will be statistically true, but the truth of the statement at the point in time when one checks to see if it is true, is effectively random.